Height
Reference Frame
What is a height above sea level?
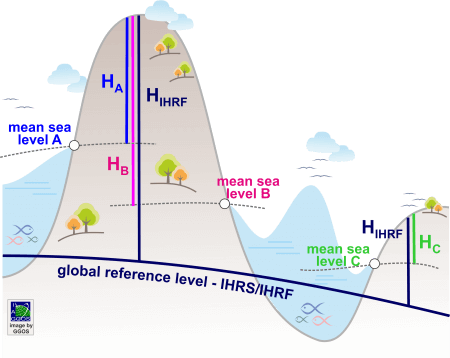
A height system is a one-dimensional coordinate system used to express the metric distance (height) of a point above a reference surface (i.e., the zero-height level). Traditionally, the reference surface is linked to the mean sea level and the heights are determined using geodetic levelling techniques. These techniques measure the distance between two equipotential or level surfaces of the Earth’s gravity field and provide the height along the curved plumb line. The mean sea level serving as the zero-height level is inferred from averaged tide gauge records over certain time intervals and the heights are determined along the so-called vertical or levelling networks. As the tide gauges register the local sea level and the vertical networks cover limited regions, these systems are known as local height systems. Presently, there are about hundred local and regional height systems in use, and they exhibit discrepancies with respect to each other up to 
2 m.
The International Height Reference System (IHRS) is a global unified height system: the zero-height level is a global equipotential surface of the Earth’s gravity field and the vertical coordinate of any point on the Earth’s surface is the level difference with respect to that global equipotential surface. Heights referring to the IHRS are consistent globally and do not depend on the local sea levels. The realisation of the IHRS is the International Height Reference Frame (IHRF): a set of reference stations homogeneously distributed over the world and with known geopotential numbers or height values referring to the IHRS.
A prominent example of the importance of the IHRS/IHRF is the recent height determination of Mount Everest in 2020. Referring this height to the Chinese height system (e.g. 
in the figure above) or to the Nepalese height system (e.g. 
) would produce different values, making difficult to decide which one is the appropriate one. To avoid discrepancies, the Chinese and Nepalese governments agreed to refer the new Mount Everest’s height to the IHRS/IHRF (e.g. 
).
The IHRS defines the equipotential surface of the Earth’s gravity field with the geopotential value 
as the global reference level. 
is understood to be the gravity potential of the geoid or the geoidal potential value. The vertical coordinate is the geopotential number 
: the potential difference between the conventional reference value W0 and the potential 
of the Earth’s gravity field at a point 
. The spatial reference of the position P for the potential 
is given by the coordinate vector 
in the International Terrestrial Reference Frame (ITRF). Thus, the IHRS is founded on the combination of a geometric component given by 
and a physical component given by the determination of 
at . Coordinates of a point attached to the solid surface of the Earth include not only the station position 
and the geopotential number 
, but also the coordinate changes with time; i.e., 
and 
. For practical purposes, coordinates can be converted to ellipsoidal coordinates latitude 
), longitude (
) and ellipsoidal height (
) and the geopotential numbers may be converted to a physical height (dynamic, orthometric or normal height).
Realization of the IHRS
Current activities oriented to the realisation of the IHRS concentrate on:
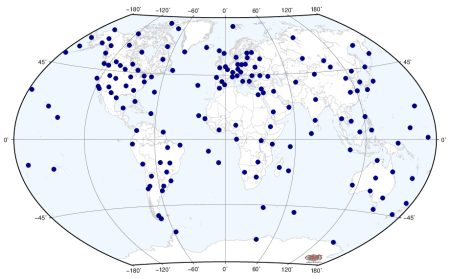
(i) designing a preliminary reference network for the IHRF;
(ii) studying strategies for the determination of precise potential values ; and
(iii) identifying/outlining the standards and conventions required to establish an IHRF consistent with the IHRS definition.
The IHRF-related activities are coordinated by the GGOS Focus Area Unified Height System under a strong cooperation with
- The International Gravity Field Service (IGFS)
- The study group “Geoid/quasi-geoid modelling for realisation of the geopotential height datum” of the Inter-Commission Committee on Theory (ICCT)
- The IAG Sub-Commission 2.2 “Methodology for geoid and physical height systems”
- The working group “Error assessment of the 1 cm geoid experiment” of the IAG Commission 2
- The joint working group “On the realisation of the International Gravity Reference Frame (IGRF)” of the IAG Commission 2
- The working group “Towards a consistent set of parameters for a new Geodetic Reference System (GRS)” of the GGOS Bureau of Products and Standards
